Measuring the polarization fraction and profile for a clumpy star-forming galaxy at $z = 3.4$
What is the origin of the Lyman-alpha emission?
The Lyman-$\alpha$ issue
Lyman-$\alpha$ (Ly$\alpha$) emission is the strongest tracer of recombining ionized hydrogen in young, star-forming galaxies, but its origin is still debated. Ly$\alpha$ arises when emitted photons scatter in neutral hydrogen, and each scattering event changes their propagation direction and frequency. Hence, the observed Ly$\alpha$ emission surface brightness and spectral profile depend on the neutral hydrogen column density, geometry, kinematics, power mechanism and on the region from which the photons are emitted. The Ly$\alpha$ emission can be powered by centrally emitted photons, significantly scattered along their paths prior to escape, or by extended star formation and cooling gas, heated by supernova explosions and galactic winds.
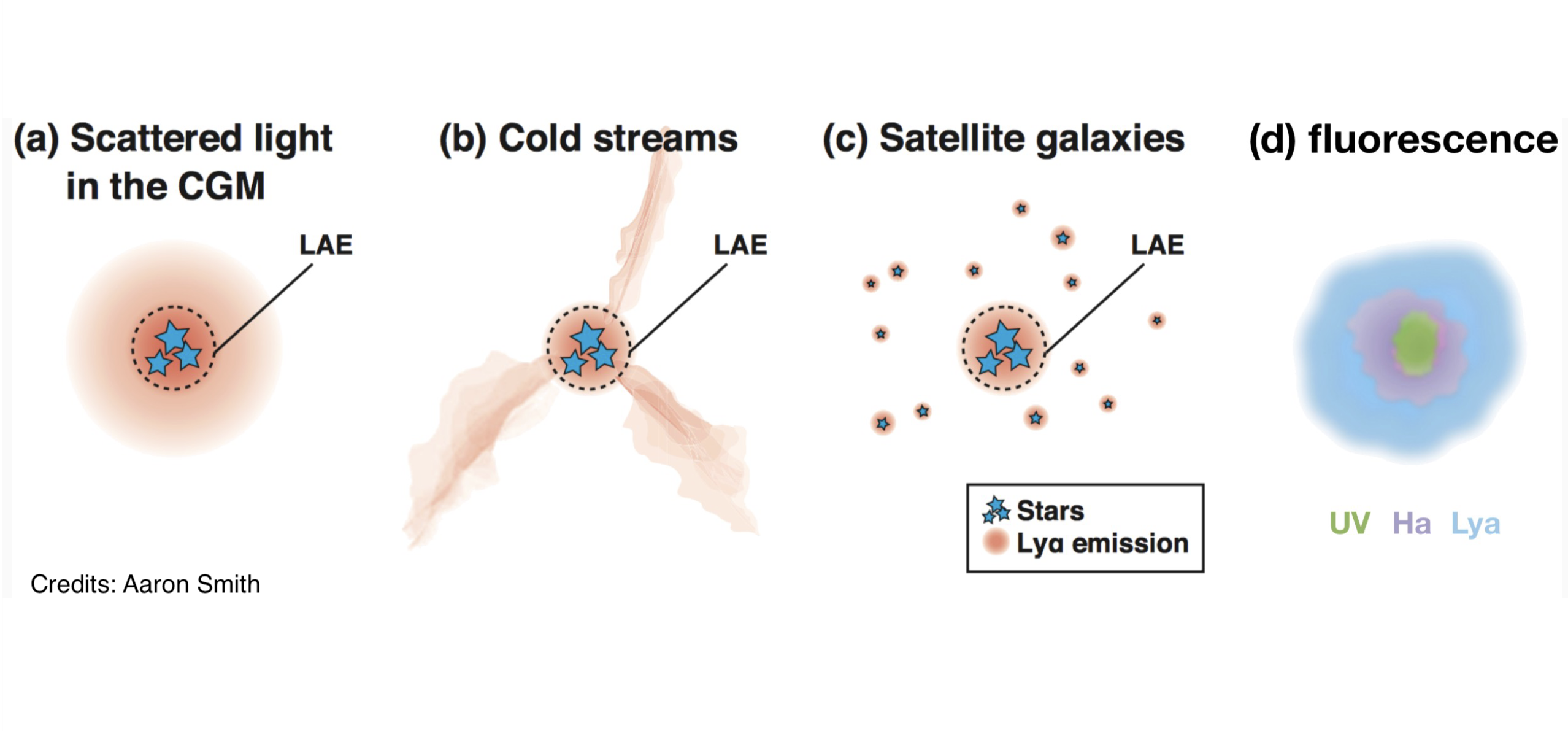
How polarization can solve it
The Ly$\alpha$ degree of polarization increases if photons are scattered in a preferential direction, and the resulting value mainly depends on two fundamental factors: the production mechanism and site where the Ly$\alpha$ photons are created, and the geometry of the gas where they scatter before escaping, being in particular sensitive to the isotropy and homogeneity of the emission and gas distribution. Due to the observational difficulty of measuring the Ly$\alpha$ degree of polarization of distant sources and the limited number of available (spectro-) polarimeters intended for extragalactic use, only a few studies that map the polarization of Ly$\alpha$ are currently present, and none of them targeted typical star-forming galaxies at high-$z$.
The target and my work
In my work we put novel constraints on the geometry of the HI region surrounding a clumpy star-forming galaxy at $z \approx 3.4$, Abell 2895a, strongly lensed into three multiple images by the cluster of galaxies Abell 2895 (image on the left). We made use of new deep (18 hours, PI: A. Zanella) VLT/FORS2 observations taken with the Polarimetric Multi Object Spectroscopy (PMOS). Our main findings are:
- We obtained upper limits of 4.6\%, 5.8\%, and 6.5\% at the $1\sigma$, $2\sigma$, and $3\sigma$ level on the Ly$\alpha$ degree of polarization. We showed that polarization constraints are complementary to those usually achieved by using only the total Ly$\alpha$ intensity and line profile, demonstrating the effectiveness of this novel technique.
- To interpret the observational constraints, we developed a Ly$\alpha$ radiative transfer model including a bipolar wind geometry (characterized by the opening angle $\theta_{\rm o, Wind}$, the radial expansion velocity $v_{\rm exp}$, and the HI column density parameters) and a central source that emits Ly$\alpha$ photons with a Gaussian profile of width $\sigma$. We assumed N_{\rm HI} $\sim 10^{20} {\rm cm^{-2}}$, $v_{\rm exp} \sim 200 {\rm km/s}$, and $\sigma \sim 150 {\rm km/s}$ and tried different $\theta_{\rm o, Wind}$ values (from 0° to 90° with steps of 15°) and simulated different line of sight angles ($\theta_{\rm LOS} from 0° to 90° with steps of 10°).
- In order to reproduce the spectral profile and shift with respect to the systemic velocity of the Ly$\alpha$ line, we needed Ly$\alpha$ photons that are created in the inner regions and that undergo several scattering events before escaping, and $\theta_{\rm LOS}<\theta_{\rm o, Wind}$ (i.e., observing in the direction of the outflow) and $\theta_{\rm o, Wind}$ > 15°$
- The results are summarized in the figure on the right, for all the cases varying $\theta_{\rm LOS}$ ($x$-axis) and $\theta_{\rm o, Wind}$ ($y$-axis): the greyscale represents the $\chi^2$ between the observations and the simulated spectra. Whiter colors express more agreement (dark cases are those where the simulated Ly$\alpha$ is not shifted with respect to the systemic velocity, and/or is narrower or wider).
Red hatched regions are canceled from the polarization constraints, as the simulated polarization is larger than the observed upper limit (at 1$\sigma$).